Лінійна функція , її властивості та графік

Теорія:

Лінійна функція — це функція, яку можна задати формулою

y=kx+b, де x — незалежна змінна, k і b — деякі числа.

Застосовуючи цю формулу, якщо відоме конкретне значення x, можна обчислити відповідне значення y.

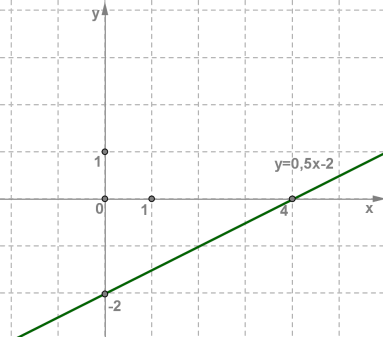
Нехай y=0,5x−2.

Тоді:

якщо x=0, тоді y=−2;

якщо x=2, тоді y=−1;

якщо x=4, тоді y=0 і т. д.

Зазвичай ці результати оформлюють у вигляді таблиці:

x	0	2	4
y	−2	−1	0

x - незалежна змінна (або аргумент), y - залежна змінна.

Графіком лінійної функції y=kx+b є пряма.

Щоб побудувати графік даної функції, нам достатньо мати координати двох точок, що належать графіку функції.

Побудуємо на координатній площині xOy точки (0;−2) і (4;0), оформлені у таблиці,  і проведемо через них пряму.

Багато реальних ситуацій описуються математичними моделями, що являють собою лінійні функції.

Приклад:

На складі було 500 т вугілля. Щодня почали підвозити 30 т вугілля. Скільки вугілля буде на складі через 2; 4; 10 днів?

Якщо пройшло x днів, то кількість y вугілля на складі (у тоннах) можна виразити формулою y=500+30x.

Таким чином, лінійна функція y=30x+500 є математичною моделлю ситуації.

За x=2 маємо y=560;

за x=4 маємо y=620;

за x=10 маємо y=800 

Однак треба враховувати, що в цій ситуації x∈N. (натуральне число)

Якщо лінійну функцію y=kx+b треба розглядати не за всіх значень x, а лише для значень x із деякої числової множини X, то пишуть y=kx+b,x∈X.

Приклад:

Побудувати графік лінійної функції:

a) y=−2x+1,x∈[−3;2] 

b) y=−2x+1,x∈(−3;2)

Складемо таблицю значень функції:

x	−3	2
y	7	−3

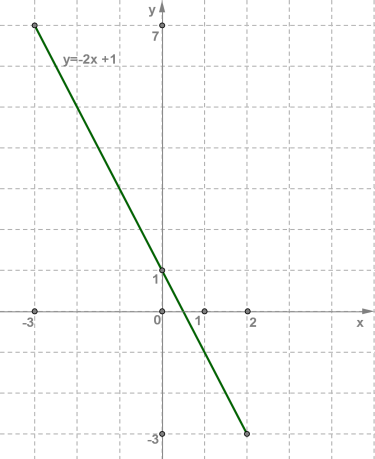
Позначимо на координатній площині xOy точки (−3;7) і (2;−3) та проведемо через них пряму.

Далі виділимо відрізок, що з'єднує позначені точки. Цей відрізок і є графіком лінійної функції y=−2x+1,x∈[−3;2].

Точки (−3;7) і (2;−3) належать даному інтервалу (квадратні дужки) та на рисунку позначені темними кружечками.

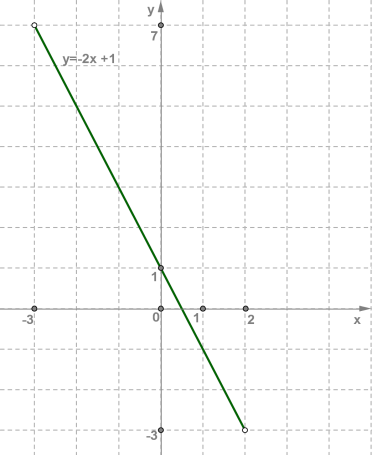
b) У другому випадку функція та сама, тільки значення x=−3 і x=2 не розглядаються, оскільки вони не належать інтервалу (−3;2) (круглі дужки).
Тому точки (−3;7) і (2;−3) на рисунку позначені світлими кружечками.

Розглядаючи графік лінійної функції на інтервалі, можна назвати найбільше і найменше значення лінійної функції.

У випадку

a) y=−2x+1,x∈[−3;2] маємо, що yнайб =7 і yнайм =−3,

b) y=−2x+1,x∈(−3;2) маємо, що ні найбільшого, ні найменшого значень лінійної функції немає, оскільки обидва кінці відрізка, у яких саме й досягалися найбільше і найменше значення, виключені з розгляду.

У ході побудови графіків лінійних функцій, можна ніби «підніматися вгору» або «спускатися з гірки», тобто лінійна функція або зростає, або спадає.

Якщо k>0, тоді лінійна функція  y=kx+b зростає;

якщо k<0, тоді лінійна функція y=kx+b спадає.